三角比と三角関数は同時に学ぼう

高校数学のカリキュラムの中でも特に不思議なところがある。
それは、数Iで三角比を学び、せっかくサインだコサインだと覚えたのに、一通り忘れただろう高校2年生の数IIで三角関数を学習することだ。
もしかすると型通りの順番で律儀に教えるのではなく、三角比と三角関数を連続して教える学校もあるかもしれない。これは実に理にかなっているし、三角関数は高校2年生にならないと絶対にわからない、などという代物では決してない。
類似した単元を一度に学ぶことにより学習効率が上がるし、また理解も深まるだろう。
今回は、三角比と三角関数を同時に学ぶことの有用性、それと三角比は単位円ではなく弧度法のグラフを使うべき理由について紹介していく。
三角比を学んでいる高校1年生、そして三角関数を学ぶ高校2年生、両方を総復習している受験生全員に対して参考にしてほしい。
なぜ三角比と三角関数を同時に学ぶべきなのか
冒頭でも話した通り、三角比は高校1年生で習うことになる。
高校に入って初めてsin、cos、tanという新しい概念を学び、大抵の場合これらの概念を用いて下記のような三角形、または単位円を使って、三角比を求めることになるだろう。
図1:三角形を使った三角比の導出
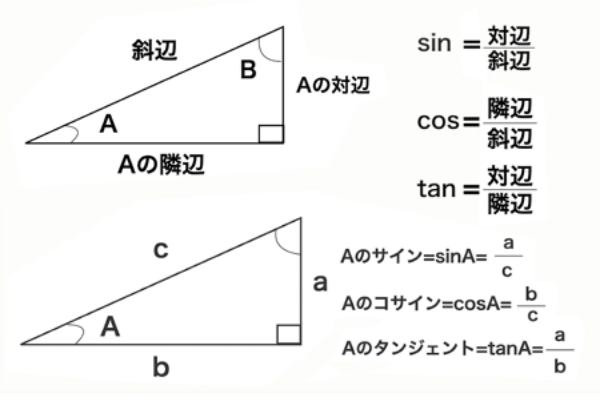
図2:単位円を使った三角比の導出
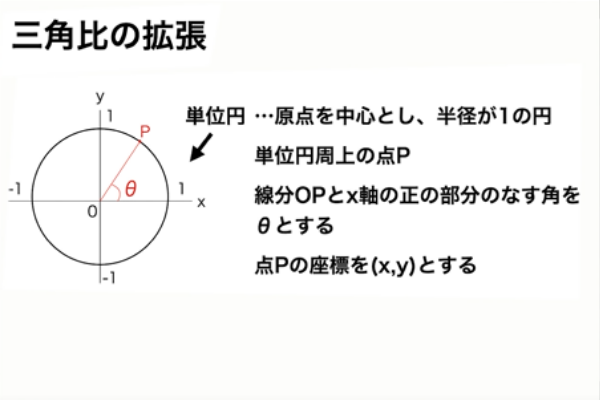
いずれも高校数学の三角比とは?三角比の相互関係や拡張も練習問題を通じて解説|StudySearchより
一見すると、これらは非常にわかりやすい覚え方のように思える。
しかし、三角形や単位円で三角比を導出するやり方はその後の汎用性に乏しく、三角関数の範囲に入ってくると逆に混乱を招く恐れがある。
わたしも長らく塾講師として三角比や三角関数を教えてきたが、苦手にしている生徒ほど単位円や三角形を使い、得意な生徒は早い段階でグラフを使っていた。
確かにθが0≦θ≦90°の範囲(つまりは三角形が描ける範囲)にあれば、図1のような三角形または図2のような単位円を書いて考えたらすぐに答えが出てくるだろう。しかし、θが0≦θ≦90°を超えて90°≦θ≦360°等となってくると、三角形を使った導出はまずできなくなる。
90°を超える場合には単位円を使うことになるが、0≦θ≦90°の時と違い、sinθとcosθってどっちがどっちになるんだっけ?どっちがマイナスになるんだっけ?と、途端に混乱してしまう人が増える。ここにtanθが出てくると頭の中の「?」は更にたくさん浮かんでくることだろう。
しかし、三角関数で学ぶサイン・カーブ(正弦曲線)、コサイン・カーブ(余弦曲線)を使えば、まず間違いなくそういった混乱を防ぐことができる。
なぜなら、サイン・カーブとコサイン・カーブ、そしてタンジェント・カーブはまったく形状が異なるからだ。
図3:サイン・カーブ
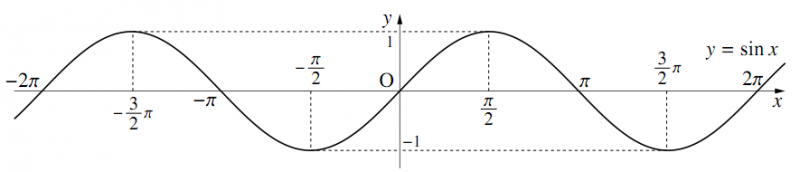
図4:コサイン・カーブ
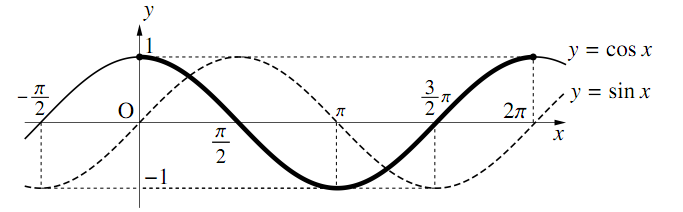
図5:タンジェント・カーブ
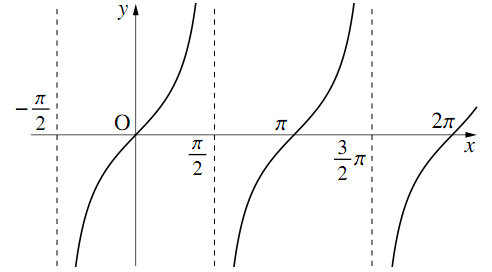
図3~5はいずれも三角関数のグラフより
サイン・カーブとコサイン・カーブは多少形状が似ていると思うかもしれないが、「0°≦θ≦360°(2π)の間でサインはゼロからスタートするのに対して、コサインは1からスタートする」とだけ覚えておけば、間違えることはない。
タンジェントはより簡単で、どこが漸近線となっていて、どこの値がゼロになるのかさえわかれば非常にシンプルなグラフである。
「これを覚えるの大変だ」「三角形、単位円のほうが簡単で良い」などと最初は思うかもしれないが、三角関数を学んだあとは単位円が出てくることはない。三角形ともおさらばである。
遅かれ早かれ上記のようなグラフを使うことになるのだから、高1で三角比を学ぶ段階で、各グラフを覚えておこう。
損はないどころか得しかない。
XX°を卒業して弧度法に慣れよう
もう一つ、学習に有用な先取りポイントを言及しておこう。
三角関数においては、XX°とは書かず、弧度法(ラジアン)を用いてsinπなどというようにπを使う。
これは記号としては円周率のπ(パイ)と全く同じ記号だが、三角関数で使うπはπ=3.1415…ではなく、π=180°を意味する。
初めは意味がわからないかもしれないが、都度180°とか45°とか書いているのが面倒くさいのでπ、π/4と表記の仕方を変えているだけだ。
慣れれば問題なく使いこなせるようになるだろう。
サイン・カーブ、コサイン・カーブにおいて覚えておくべき角度は究極的には下記のものだけとなる。
π=180°
π/6(30°)
π/4(45°)
π/3(60°)
π/2(90°)
あとはこれの応用(倍数)で覚えていけばいい。
例としてサイン・カーブで考えてみよう。
サイン・カーブは図3にある通り、0°の時sin0°=1、90°、つまりsin π/2=1へと次第に値が大きくなっていき、その後はまた180°、つまりsin π=0に向かって下がっていく。
サイン・カーブを描くときは、90°までは値を徐々に上げていき、90°以降は180°に向かって逆の順番で徐々に値を下げていけばいい。
sin π/2までは徐々に上がっていき、先ほど伝えた覚えておく4角度だけ値を頭に入れる。
sin π/6(30°)= 1/2
sin π/4(45°)= √2/2
sin π/3(60°)= √3/2
sin π/2(90°)= 1
その後sin πに向かって徐々に値が下がっていく。
こちらも角度は上の4つの倍数であることがわかるだろう。
sin 3π/2 (120° = 90°+30°)= √3/2
sin 3π/4 (135°= 90°+45°)= √2/2
sin 5π/2 (150°=90°+60°)= 1/2
sin π (180°=90°+90°)= 0
この調子で180°≦θ≦360°は、マイナスの範囲で同じことをやっていけばよい。
文章で書くと非常にわかりにくいかもしれないが、実際に自分でグラフを書き、π/6(30°)、π/4(45°)、π/3(60°)、π/2(90°)と30°刻み、または45°刻みで0°≦θ≦360°のグラフを書いていけば、言わんとしていることがわかるはずだ。
便宜上「グラフを描く」としたが、曲線というよりもπ/6(30°)、π/4(45°)、π/3(60°)、π/2(90°)が階段の段だと思えばわかりやすいだろう。
コサイン・カーブも同様にこの刻みで覚えておこう。
タンジェントはπ/2、3π/2…という刻みで漸近線を描き、0、π、2π…がゼロになるようにグラフを書けば良い。正直なところ、タンジェントは問題になりにくいため、三角関数を理解する上で重要なのは、ほぼサインとコサインのグラフを如何に早く頭に入れるかに懸かっている、と言っていいだろう。
三角比で覚えるべきは3つの定理・公式だけ
グラフを用いた考え方だけだけでなく、三角比で学ぶことのほとんどは三角関数で導出することができる。
例えば、三角比で学ぶ下記のような式をみてほしい。
三角比しか学んでいない人は、この等式を丸暗記する必要があるかもしれないが、三角関数で習う加法定理を使えば問題なく自分で導出することができる。いちいち暗記する必要はない。
図6:三角比で覚える関係式
(タンジェントだけは加法定理ではなくtanθ = sinθ / cosθを使う。なぜならtan90°の値が存在しないため、加法定理が使えないためだ)


いずれも数スタ【三角比】180-θ、90-θ、90+θの公式の覚え方と使い方をイチから!
こちらはもれなく加法定理で導出できるため、覚える必要はない。
覚えるべきは加法定理だけだ。
三角関数で習う2倍角の公式も加法定理から導ける。半角の公式などは導出するよりも覚えたほうが早そうだが、そもそも試験ではあまり出ない。導出の仕方さえ覚えておけば事足りる。
とういうことで、三角比で学ぶことの多くは三角関数を学べばおのずと導出することができるのだ。こういった理由から、三角比から連続して三角関数を学んだほうが理解がしやすく、学習効率も上がるだろう。
三角比で学ぶ内容のうち、三角関数で出てこないのは「正弦定理」「余弦定理」「三角比を用いた三角形の面積の出し方」の大きく言えばこの3つだけだ。
逆に言うと、三角比を学習する際はこの3つの定理、算出式だけは忘れないように覚えておこう。
残りは三角関数のグラフと加法定理を学べば公式を暗記する必要はない。
編集後記
わたしの職場の後輩に京大出身の秀才君がいる。
まだ入社して半年ちょっとしか経っていないが、すでにそのあふれんばかりの優秀さを発揮しており、上司であるわたしは日に日に自身の存在意義と担当の業務を失っている。
なんとも嬉しいばかりだ。
さて、彼と話していて思うのは、頭の良い人は物事の整理の仕方がうまい、ということだ。
仮にも上司であるので色々と教えることになるのだが、教えたことの間に類似性を見出して、点と点を線で結んでいくようなイメージで新しいことを学び吸収していく。
数学に限らずどの教科でもそうだが、単元や内容を整理したり、うまくカテゴライズしたり、共通点を見出すことで、学んだことが単純な1 + 1 = 2 ではなく、1 + 1 = 3になるような相乗効果を生み出す場合がある。
結果として学んだ後に気づくことも多いため、学んでいる時に意識することは難しいかもしれないが、常に意識的であることをおすすめしたい。
そういった意味では、学校で習う順番が最適解だと思わないほうが良い。
今回は三角比と三角関数を一緒に学ぶことの有用性を話したが、三角関数もまた「関数」であるわけで、ほかの関数(2次関数、指数関数、対数関数、微分積分もついでに入れちゃおう)と一緒に一気に学ぶのも効率的かもしれない。
究極的に「関数」と呼ばれるものは高校数学ではxy平面(2次元)、もしくはxyzの立体空間(3次元)に落とし込むことになる。
このような共通点を用いて、それぞれの単元のグラフの形状を意識しながら学んでいくと、理解が深まるかもしれない。
機械的に各単元を学習するのではなく、それぞれの単元にある共通概念を見出しながら整理して学んでいくと、体系的な知識として自分の中に根付いていくことになるだろう。

