数学 – 単元ごとに「求められる技能」を意識する –

文系であろうと理系であろうと、大学入試において数学は非常に重要な科目であり、数学の出来が合否を分けると言っても過言でない、とこれまで力説してきた。

また、大学としても数学ができる学生を露骨に優遇、歓迎しているという最近の大学受験動向についても併せて紹介してきた。詳しくはこちらの記事にあるので、興味があれば読んでみて欲しい。

今回は高校数学というものを、単元別ではなく、求められる技能別に分けて考えることの重要性を紹介していく。

必要となる技能を意識することで、数学の学習効果は格段に改善するだろう。

数学に求められる3技能

独断と偏見で恐縮であるが、高校数学の理解に必要となる技能は計算力、解法パターン適用力、概念理解力の3つである、とわたしは考えている。

高校数学のすべての単元において、理解するための能力はこの3つに集約される。
それぞれの技能を意識しながら学ぶことで、理解力が一層深まることだろう。

では、それぞれの単元において、この3つのうちどの技能を意識しながら学べば良いだろうか。

下記のリンクでは、教科書等を発行している大日本図書の「領域・単元別学習内容系統表（小・中）」という図を見ることができる。
https://www.dainippon-tosho.co.jp/introduction2021/contents/files/r3math_keitou.pdf

こちらの図を参考にし、まずは数学I～数学Cまでの単元において必要とされる技能を3つの技能に振り分けた。

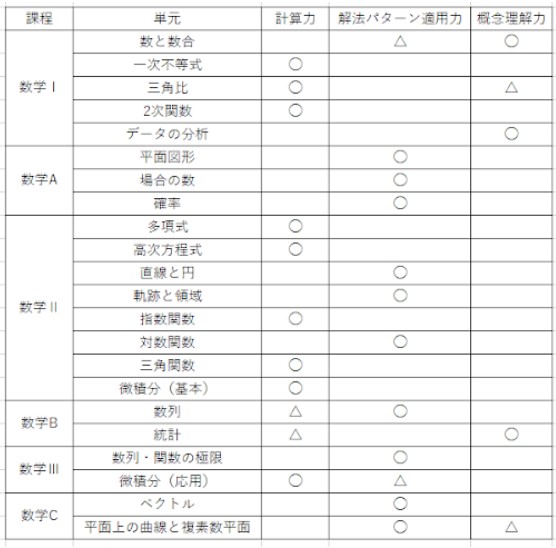
◯が最も求められる技能、△が必須では無いが次いで必要になると思われる技能だ。
どの技能が必要とされているかを表す表であるため、◯、△共に記載がなくとも、その技能は必要ないという意味ではないことに注意して欲しい。

では、どの単元にどの技能が必要とされるかを少し確認してもらったところで、この3つの技能がどのようなものであるかをそれぞれ見ていこう。

数学的技能：計算力

計算力とは「計算を素早く、正確に行う能力」である。
3つの技能の中で最も簡単に説明できる技能だ。

計算力があるだけで解ける単元に関しては、計算方法さえわかっていればよい。
突き詰めれば四則計算をするだけとも言えるので、ミスさえしなければ正解を導くことができる。入試問題で出てきた場合にはラッキー問題と思って良いだろう。

ただし、問題が難しくなればなるほど計算ミスが起こりやすくなり、細かい計算が続くほど時間の浪費が起こる可能性もあるので注意が必要だ。

計算力を鍛えるには、問題演習の際に「如何に速く、正確に解くか」を意識しながら取り組むことだ。演習時はただ問題を解くだけに留まらず、計算力を鍛えるという目的意識をもって取り組もう。

また、そういった正攻法だけではなく、計算ミスの回避術や時間短縮術も併せて身につけてほしい。

ものすごく簡単な例をいえば、「6422322*38+6422322*62」を計算する場合、もちろん「6422322*38」と「6422322*62」の結果を足し合わせることで答えを出すこともできるが、分配法則を知っていれば「6422322*100」だけを計算すればいいことになり、一瞬で計算できる。

ここまで露骨な問題は少ないが、「工夫すれば簡単に解けるようになっているのがわかりますか？」と訴えかけてくるような問題はままある。

いきなり計算を進めるのではなく、少しでも時短することを意識してみよう。時短は概ね計算ミスを抑えることにも繋がる。

数学的技能：解法パターン適用力

解法パターン適用力は、「解法がパターン化されている問題に、きちんとパターンをあてはめて解答を導く力」だ。

このようにやれば解ける、この定理・公式を使えば一発で答えが出る、というように、一度わかってしまえばなんてことのない問題がある。こういった「一見難しそうだが、わかってしまえば難なく解ける問題」の解法を、しっかりと理解・記憶しておき、試験で自由自在に使いこなすことができるかどうか、という技能を指している。

公式を当てはめる、定理が使える状態に持っていく、といった具合に解法さえ浮かべば、後はそれに適した計算をしていくだけになる。

この手の問題はたいてい計算自体もパターン化されているため、計算ミスや予想外に時間がかかるというようなことも起きにくい。適切なベルトコンベアに問題を乗せれば、後は流れ作業で答えがアウトプットされる、というようなイメージだ。

例として、「2の2022乗は何桁になるか」を考えてみよう。
素直に計算するのであれば計算力が問われる問題になるのだが、まず間違いなく計算ミスをするし、そうでなくとも答えを出すのに時間がかかりすぎるため、全くもって得策ではないアプローチである。

ちなみにエクセルで計算しようとしたが、エラー表示になった。Googleで計算しても結果が「Infinity」となったので、まともに計算するような問題ではないことがわかる。

ちなみにべき乗の計算ができるサイトで調べたところ、一応結果は出たが、計算過程は省略されていた。

わざわざこんなことをせずとも、普通に考えれば計算力を問われている問題ではない、ということはわかるだろう。

ここで問われているのは解法パターン適用力だ。
この問題をパッとみた瞬間に「常用対数を使った解法パターンに落とし込むこと」ができるかどうかがポイントになる。

• 解き方を少し具体的に説明すると、以下のようになる。
  整数nを用いて、10のn乗<2の2022乗<10の（n+1）乗とおく。
• 全辺で常用対数を取れば、n<2022×log2<n+1となり、2022×log2を求める
• 2022×log2＝608.68、つまりはn=608となるので、2の2022乗は609桁

結果を出すまでに行った計算は実質2022×log2だけだ。
しかも、常用対数の暗記は入試では求められていないため、log2は「log2=0.3010とする」といった具合に親切にも提示されている。

知っていれば解ける問題は数多くあるが、こういった類の頻出問題や有名問題は、解法を理解し、使いこなせなければ試験では使えない。

そのため、解法パターン適用力が強く求められる単元においては「こういう問題にはこの解法パターン」ということを、強く意識しながら学習していくべきだろう。

数学的技能：概念理解力

概念理解力というものを独立して技能とするか少し迷ったが、入れることとした。
というのも、「自分が今何をやっているのか」「何を求めればよいのか」を理解していないのは致命的であり、大体にして数学を苦手としている人はこの状態にあるからだ。

当たり前のことではあるが、すべての単元において「概念を理解すること」は非常に重要だ。前述した計算力も解法パターン適用力も、概念を理解してこその技能である。

中でも特に概念理解力が必要である単元が、「数と数合」や「統計」などである。

「ある命題の真偽を考える場合、その対偶の真偽が分かれば、元の命題の真偽もわかる」といった学習を理解する際、そもそもとして「対偶とは何か？」「真偽を判定する際の必要十分条件とはなにか？」といった具合に、必要な前提知識が理解できていなければ学習を進めるのは難しいだろう。

また、対偶の真偽を考えたり、必要十分条件を検証したりするのに多少の計算は必要なものの、そもそも、「なぜ対偶の真偽が分かれば元の命題の真偽がわかるのか」「必要十分条件を満たすかどうかを考えることがなぜ真偽の判定に関係するのか」ということをきちんと理解しないことには、何を求められていて、何をすれば良いのか皆目見当がつかなくなってしまう。

「√3が無理数であることを証明しなさい」という問題があったとしよう。
この問題を前にして「√3が無理数だなんて当たり前」としか考えられないようであれば、この手の問題に太刀打ちできない。

√3が無理数である→有理数でない→有理数であると仮定する→背理法で矛盾を導く

この問題に関しては上記のような思考で解いていくのであるが、こういった考え方ができるのかどうか、ひいては当たり前に受け入れていることに対しても、いざとなればその「当たり前」を証明できること、つまり概念的な理解ができているのかどうかが非常に重要になる。

この項目の説明をみてもらっても分かる通り、ここでは数字も計算もほとんど出てこない。
そして、上の表で概念的な理解は◯が少ないという意味でも軽視されがちな部分ではある。
しかし、本質的に概念的な理解を大前提として計算力、解法パターン適用力があるともう一度しっかりと理解してもらいたい。最も重要な技能は「概念的な理解」なのだ。

「円周率が3.05よりも大きいことを証明せよ」と問うた東大数学は、今や伝説といってもいいだろう。数学の勉強において、普段は自明としているような根本的な部分を問うてくるのが、東大京大などの最難関国立大学の数学の問題だ。

この問題から「どういった能力をもった学生を入学させたいのか？」は、容易に読み取れるのではないだろうか？

編集後記

高校数学では計算力と解法パターン適用力が強く求められるとの話を展開してきたが、最後に記したように、最も重要なのは概念的な理解力だ。

前者2つの技能だけで大学数学に臨んでも全く太刀打ちできない。

というのも、大学以降では複雑な計算は機械にやらせればいい。
というか、そもそもそ計算式は数字ではなく文字（文字式）で行われるため、計算する機会はあまりないのだ。

大学数学とはなにかというと、ひたすらに証明を行っていく作業なのだ。
Aは、Bだから、Cだよね（証明1）ということは、DはEになる（証明2）からFが言えて（証明3）、つまるところGということだよね（答え、というか結論）。といった感じだ。
もちろん数学の分野によって違いはあるだろうが、証明の上に証明を重ねていき、最終的な答え（と言う名の結論）を導き出す。大体の場合、大きく見ればこのような流れになっている。

ちょっとした笑い話なのだが、大学時代に解析学という、およそ誰も取らないような授業を、数学好きかつ自称数学ができると自負していたわたしは受講した。

しかしその授業が始まってから終わるまでの半年間、全12、3回の講義の内容を私は1ミリとして理解することができなかった。全くのゼロである。

宇宙人に連れ去られて、彼らがずっと理解できない言語でなにかを言っているのをただ聞いている、というような状況だった。

このとき初めて、中高で「数学がわからない」と言っていた人の気持ちがわかった。確かに一ミリも理解ができないのであればやる気もなくなるよな、と少しだけ人に優しくなれた気がする。

後日談だが、解析学は最後にレポート（と言う名の問題を解く課題）を提出することになっていた。夜中に発狂しながら必死に課題をこなし提出したら、どうも正解だったらしく、無事にA（当時の最高評価）をもらえた。「あの解析学でAを取った！やっぱイズミすげー！！」と周りにはえらく感心されたが、全くもって内容を理解しているわけではないので、正直あまり触れてほしくない、というのが私の本心である。

数学の概念理解力こそ、真に磨いておくべき技能だ。